What is Big O notation and how to assess the efficiency of your algorithm using the Big O notation?

Big O notation is a way to describe how fast an algorithm runs or how much space it needs, especially as the input size gets really large. It focuses on the main factor that affects the algorithm's performance, ignoring smaller details that don't matter as much when the input is very big.
Here is a simple example. We want to find the string 'cat' in an array.
public class FindString {
public String findCat(String[] arr) {
int a = 0; // O(1)
int b = 2; // O(1)
for(int i=0; i<arr.length; i++) { // O(n)
if("cat".equals(arr[i]) { // O(n)
System.out.println("Found cat"); // O(n)
}
}
int c = a + b; // O(1)
}
}How can we assess the performance of the findCat method? You may say that we can calculate the run time of this method using the end-time to subtract the beginning time. It's a way to do that, but not perfect as different machines would have a different runtime because there are so many factors that affect the runtime of this function. That's where Big O notation comes in.
For our example, there is a for loop within the findCat method, let's assume that one line of code within this method runs 1 unit of time. So the time complexity of this method can be noted as O(3n+3), which is a linear time complexity, n stands for the length of the input array. But normally we just change it to O(n).
To get the Big O of an algorithm, here are four rules:
- Worst Case: for example, in the previous example, the worst case would be that the cat is the last item in the array.
- Remove Constants: for example, if the notation is O(2n + 10), we just revise it to O(n).
- Different Terms for Inputs: for example, if there are two arrays as parameters and they are being iterated within the method one by one, then the Big O notation would be O(m + n), m and n stand for the length of the first and second array.
- Drop Non-Dominants: for example, we have a notation of O(n^2 + n), after removing the non-dominants, the Big O notation would be O(n^2).
Common Big O Notations:
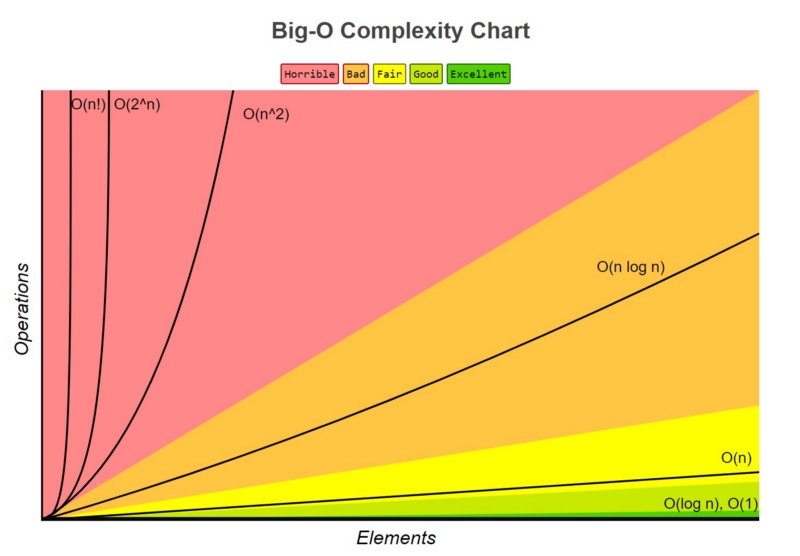
- O(1): Constant time. The algorithm takes the same amount of time regardless of the input size.
- O(log n): Logarithmic time. The running time grows slowly as the input size increases, like in binary search.
- O(n): Linear time. The running time increases directly with the input size, like in a simple loop through an array.
- O(n log n): Linearithmic time. Slightly more complex, often seen in efficient sorting algorithms like mergesort.
- O(n^2): Quadratic time. The running time grows quickly with the input size, typical in nested loops like in bubble sort.
- O(2^n): Exponential time. The running time doubles with each additional input element, common in algorithms that solve problems by trying all possible solutions, like the naive approach to the traveling salesman problem.
- O(n!): Factorial time. The running time grows extremely fast. You are adding a loop for every element.
Compare performance using Big O notation
Here is another example that we are using to sort a list of numbers in two different algorithms and compare their performance.
Imagine you have a list of numbers that you want to sort in ascending order. We'll compare two sorting algorithms: Bubble Sort and Merge Sort.
Here's a simplified version of Bubble Sort in Java:
public class BubbleSort {
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap arr[j] and arr[j + 1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
bubbleSort(arr);
System.out.println("Sorted array: ");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
Time Complexity: Bubble Sort has a time complexity of O(n^2). This means that if the array has n elements, the time it takes to sort the array grows quadratically as the input size increases.
Here is an implementation of Merge Sort in Java:
public class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
// Recursively sort the two halves
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// Merge the sorted halves
merge(arr, left, mid, right);
}
}
public static void merge(int[] arr, int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
// Create temporary arrays
int[] leftArray = new int[n1];
int[] rightArray = new int[n2];
// Copy data to temporary arrays
System.arraycopy(arr, left, leftArray, 0, n1);
System.arraycopy(arr, mid + 1, rightArray, 0, n2);
// Merge the temporary arrays
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (leftArray[i] <= rightArray[j]) {
arr[k] = leftArray[i];
i++;
} else {
arr[k] = rightArray[j];
j++;
}
k++;
}
// Copy remaining elements of leftArray
while (i < n1) {
arr[k] = leftArray[i];
i++;
k++;
}
// Copy remaining elements of rightArray
while (j < n2) {
arr[k] = rightArray[j];
j++;
k++;
}
}
public static void main(String[] args) {
int[] arr = {64, 34, 25, 12, 22, 11, 90};
mergeSort(arr, 0, arr.length - 1);
System.out.println("Sorted array: ");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
Time Complexity: Merge Sort has a time complexity of O(n log n). This means that if the array has n elements, the time it takes to sort the array grows in proportion to 𝑛log𝑛.
Summary
- Bubble Sort:
- Time Complexity: O(n^2)
- Suitable for small or nearly sorted arrays but inefficient for large arrays.
- Merge Sort:
- Time Complexity: O(n log n)
- Efficient for large arrays and preferred for its better performance on average.
This example illustrates how Big O notation helps compare the efficiency of different algorithms, especially as the size of the input grows. For a small list, both algorithms might perform adequately, but for large lists, Merge Sort will be significantly faster than Bubble Sort.